how to find normal vector

Normal Vector

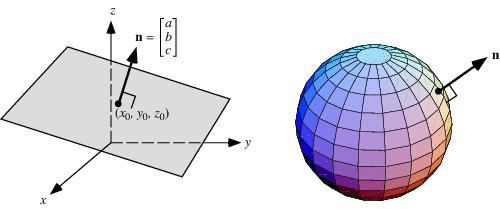
NormalVector

The normal vector, often simply called the "normal," to a surface is a vector which is perpendicular to the surface at a given point. When normals are considered on closed surfaces, the inward-pointing normal (pointing towards the interior of the surface) and outward-pointing normal are usually distinguished.

The unit vector obtained by normalizing the normal vector (i.e., dividing a nonzero normal vector by its vector norm) is the unit normal vector, often known simply as the "unit normal." Care should be taken to not confuse the terms "vector norm" (length of vector), "normal vector" (perpendicular vector) and "normalized vector" (unit-length vector).

The normal vector is commonly denoted or , with a hat sometimes (but not always) added (i.e., and ) to explicitly indicate a unit normal vector.

The normal vector at a point on a surface is given by

(1)

where and are partial derivatives.

A normal vector to a plane specified by

(2)

is given by

(3)

where denotes the gradient. The equation of a plane with normal vector passing through the point is given by

(4)

For a plane curve, the unit normal vector can be defined by

(5)

where is the unit tangent vector and is the polar angle. Given a unit tangent vector

(6)

with , the normal is

(7)

For a plane curve given parametrically, the normal vector relative to the point is given by

To actually place the vector normal to the curve, it must be displaced by .

For a space curve, the unit normal is given by

			(10)
			(11)
			(12)

where is the tangent vector, is the arc length, and is the curvature. It is also given by

(13)

where is the binormal vector (Gray 1997, p. 192).

For a surface with parametrization , the normal vector is given by

(14)

Given a three-dimensional surface defined implicitly by ,

(15)

If the surface is defined parametrically in the form

			(16)
			(17)
			(18)

define the vectors

(19)

(20)

Then the unit normal vector is

(21)

Let be the discriminant of the metric tensor. Then

(22)

Wolfram Web Resources

Mathematica » The #1 tool for creating Demonstrations and anything technical.	Wolfram\|Alpha » Explore anything with the first computational knowledge engine.	Wolfram Demonstrations Project » Explore thousands of free applications across science, mathematics, engineering, technology, business, art, finance, social sciences, and more.
Computerbasedmath.org » Join the initiative for modernizing math education.	Online Integral Calculator » Solve integrals with Wolfram\|Alpha.	Step-by-step Solutions » Walk through homework problems step-by-step from beginning to end. Hints help you try the next step on your own.
Wolfram Problem Generator » Unlimited random practice problems and answers with built-in Step-by-step solutions. Practice online or make a printable study sheet.	Wolfram Education Portal » Collection of teaching and learning tools built by Wolfram education experts: dynamic textbook, lesson plans, widgets, interactive Demonstrations, and more.	Wolfram Language » Knowledge-based programming for everyone.